Setting Up Symbol Server in Debugger
Debug symbols allow you to have better debugging sessions. They have information about the functions contained in executables and dynamic libraries and provide you with information to get clean call stacks. A Symbol Server allows the debugger to load the correct symbols, binaries and sources automatically without forcing users to download large debugging files. The server functions like Microsoft's symbol server so the documentation there can be useful.
Note that because released Electron builds are heavily optimized, debugging is not always easy. The debugger will not be able to show you the content of all variables and the execution path can seem strange because of inlining, tail calls, and other compiler optimizations. The only workaround is to build an unoptimized local build.
The official symbol server URL for Electron is
https://symbols.electronjs.org.
You cannot visit this URL directly, you must add it to the symbol path of your
debugging tool. In the examples below, a local cache directory is used to avoid
repeatedly fetching the PDB from the server. Replace c:\code\symbols with an
appropriate cache directory on your machine.
Using the Symbol Server in Windbg
The Windbg symbol path is configured with a string value delimited with asterisk
characters. To use only the Electron symbol server, add the following entry to
your symbol path (Note: you can replace c:\code\symbols with any writable
directory on your computer, if you'd prefer a different location for downloaded
symbols):
SRV*c:\code\symbols\*https://symbols.electronjs.org
Set this string as _NT_SYMBOL_PATH in the environment, using the Windbg menus,
or by typing the .sympath command. If you would like to get symbols from
Microsoft's symbol server as well, you should list that first:
SRV*c:\code\symbols\*https://msdl.microsoft.com/download/symbols;SRV*c:\code\symbols\*https://symbols.electronjs.org
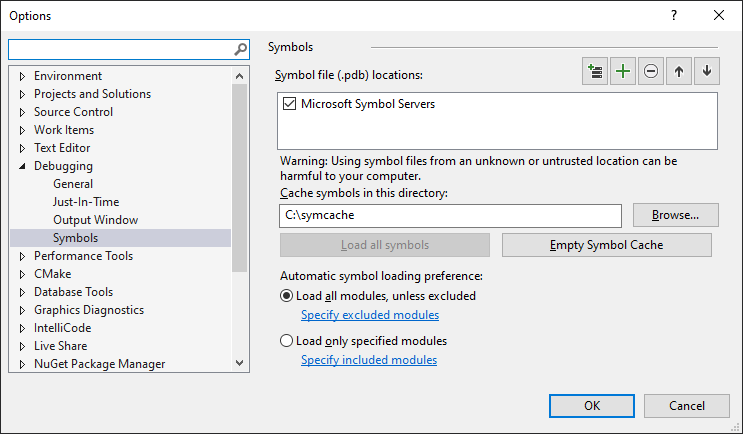
Using the symbol server in Visual Studio
Troubleshooting: Symbols will not load
Type the following commands in Windbg to print why symbols are not loading:
> !sym noisy
> .reload /f electron.exe